Truncated division 和 Euclidean division
之前一直不太理解 rust 语言中原始类型中的数值类型取模运算(mod)和除运算(division)单独提供 rem_euclid 和 div_euclid 的原因。
数学定义:
q,r∈Za=nq+r∣r∣<∣n∣
在编程语言中,实现除运算根据运算取整的时候采用何种策略来区分有五种实现。
q=[na]
r=a−n[na]
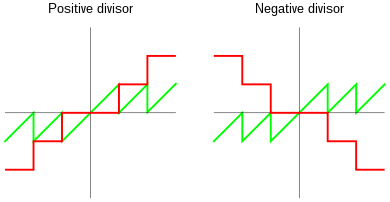
q=⌊na⌋
r=a−n⌊na⌋
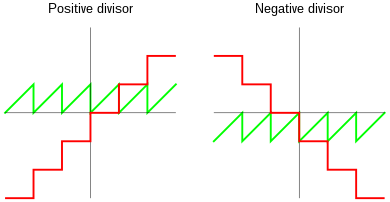
q=sgn(n)⌊∣n∣a⌋={⌊na⌋⌈na⌉if n>0if n<0
r=a−∣n∣⌊∣n∣a⌋
q=round(na)
r=a−nround(na)
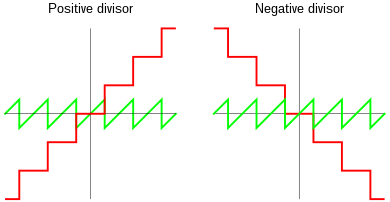
q=⌈na⌉
r=a−n⌈na⌉
我常用的语言中:
- rust 的
rem 和 div 采用的 Truncated division 实现方案。
- rust 的
rem_euclid 和 div_euclid 采用的 Euclidean division 实现方案。
- javascript 的
rem( % ) 和 div ( / )采用的 Truncated division 实现方案。
Reference


